パチンコの回転率について本当のことを教えます！！

これから紹介する、「回転率の公式」にも深く関わってくることに、一般入賞口というものがあります。

一般入賞口とは、ヘソ入賞口以外のその他の入賞口のこと。

そして今、これに関する問題がパチンコ業界を大きく揺らしているのです。

よって、先ずはこの問題に少し触れておくことにしましょう。

最近の一般入賞口における釘調整問題について

パチンコを普段打っている人なら分かると思いますが、ヘソ以外のその他の入賞口に玉が入ることはめったにありませんよね。

「なんでこんな役立たずなものが付いてるんだ？」って思っていませんでしたか？

パチンコメーカーは新台をリリースする前に、保通協という所で検査を受けます。

これにパスしないとメーカーにパチンコ台の設置許可が下りないのですが、実はこの時に、一般入賞口が活躍していたのです。

普段、私達が打っているパチンコ台は、大当たり時に出玉が片寄っています。通常時にはどんどん持ち玉が吸い込まれて行き、大当たりで連チャンして、ドカンと玉が増えるような感じですよね。

みんなこれが当たり前だと思っていたのですが、実は間違っていたんです。

通常時でも一般入賞口にもっと入賞し、玉持ち良く遊技できるというのが本来の正しい姿だったのです。

つまりパチンコメーカーは、保通協検査時に一般賞球口の釘を開けヘソ釘を締めて、「『通常時の戻り玉数』と『大当たり出玉数』の比率」を操作し検定を通過させ、ホール納品時にその逆の調整をしていたのです。

ちなみに、この「『通常時の戻り玉数』と『大当たり出玉数』の比率」については、公安委員会規則で以下のような規定があります。

遊技球の試射試験を１０時間行つた場合において、獲得する遊技球の数のうち役物の作動によるものの割合が７割（役物が連続して作動する場合における当該役物の作動によるものの割合にあつては、６割）を超えるものでないこと。

検定時の状態ではヘソ入賞が極端に少なく、とても営業に耐えうるものではないので、ホール導入時に改めてヘソ釘を開け一般入賞口を締めているのです。

実は、長年に渡って警察はこのことを知りつつも、黙認してきたのでした。ところが、最近、急にこの問題に厳しく言及し始めたんです。

どういうことかというと、要するに警察は、検定時と同じ状態でパチンコ台を出荷し営業しなさいと言ってきているのです。

この背景には、カジノ合法化の動きや、ギャンブル依存症の問題などがあるのではないかと思われます。

警察は、現在ホールにあるような高射幸性のパチンコ台ではなく、大当たり出玉だけに頼らない低射幸性のパチンコ台を目指したいのでしょう。

これから出てくるパチンコ台は、新基準に合わせた、今までにないような高ベースのものになっていくものと思われます。

2016年はパチンコ業界にとって、非常に大きな変革の年になるのではないでしょうか。

回転率の公式とは？

さて、話を回転率の式の方に戻しましょう。

パチンコ玉は1個4円で貸し出され、1000円で250個分の遊技を行うことができます。ここで仮に、あなたが「1000円あたりデジタルが20回転するパチンコ台」を打っているとします。

このパチンコ台の要件としては、ヘソ入賞時の戻り玉個数は3個で、その他の賞球口は完全に潰されているものとします。

この時、このパチンコ台のヘソ入賞確率はどのようになるか？
以下具体的な計算をしてみることにしましょう。

先ずは、この場合ヘソ入賞からの戻り玉数は60個。最初に持っていた250個と合わせて、全部で310個の玉を消費しているのが分かります。

よって、310個の玉を打ち込んでヘソに入る玉が20個ということ。これを確率に直すと、20/310、つまり1/15.5。

15.5個につき1個の玉が、ヘソに入賞していることになります。

これを一般化したものが、以下の式となります。

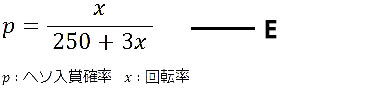
（参考）パチンコ用語

この式を元にした「回転率とヘソ入賞確率」の関係表が以下になります。（主要数値のみ）

回転率 ⇒ ヘソ入賞確率 早見表

回転率	ヘソ入賞確率
10	1/28
11	1/25.7
12	1/23.8
13	1/22.2
14	1/20.9
15	1/19.7
16	1/18.6
17	1/17.7
18	1/16.9
19	1/16.2
20	1/15.5
21	1/14.9
22	1/14.4
23	1/13.9
24	1/13.4
25	1/13
26	1/12.6
27	1/12.3
28	1/11.9
29	1/11.6
30	1/11.3
31	1/11.1
32	1/10.8
33	1/10.6
34	1/10.4
35	1/10.1
36	1/9.9
37	1/9.8
38	1/9.6
39	1/9.4
40	1/9.3
41	1/9.1
42	1/9
43	1/8.8
44	1/8.7
45	1/8.6
46	1/8.4
47	1/8.3
48	1/8.2
49	1/8.1
50	1/8

再び式 Eに戻ってみましょう。

この式を、回転率 x について解いてみます。以下が、その式となります。

（参考）パチンコ用語

この式を元にした「ヘソ入賞確率と回転率」の関係表が以下になります。（主要数値のみ）

ヘソ入賞確率 ⇒ 回転率 早見表

ヘソ入賞確率	回転率
1/4	250
1/5	125
1/6	83.3
1/7	62.5
1/8	50
1/9	41.7
1/10	35.7
1/11	31.3
1/12	27.8
1/13	25
1/14	22.7
1/15	20.8
1/16	19.2
1/17	17.9
1/18	16.7
1/19	15.6
1/20	14.7
1/21	13.9
1/22	13.2
1/23	12.5
1/24	11.9
1/25	11.4
1/26	10.9
1/27	10.4
1/28	10.0

ここで紹介した二つの式は、公式と呼べるほど大げさなものではないかもしれませんが、パチンコに関する数値計算に於いて、非常に重要な式であるので、敢えて公式と呼ばせて頂きました。

回転率の公式に関する注意点

前項の考察は、一般入賞口が潰されているという仮定で行われています。

しかし、これから出てくるであろう新機種に於いては、この仮定が通じないものと思われます。

つまり、どうしても一般入賞口からの戻り玉数を考慮に入れなければならなくなるのです。

一般入賞口からの戻り玉数を考慮した回転率の公式については、今後のコラムにて取り扱う予定でいます。

さてここではもう一つ、重要なテーマをお話ししておかなければなりません。

前章では、ヘソ入賞確率と回転率の関係について考察しました。

ここで、改めてヘソ入賞確率の本質に迫ってみようと思います。

パチンコ玉の流れを確率的に考える

前回のコラムで、「パチンコ台に於いては、玉の動きは『力学的』に考察しなければいけないが、玉の流れに関しては『確率的』に考えなければならない」と述べました。

（参考）パチンコ玉は釘の間隔が広い方に流れていく

パチンコ盤面に打たれた釘のゲージ配列は、基本的に「釘で出来た小さな三角形」の集合体となっています。

その一つの三角形から、パチンコ玉が流れてく量は、確率的に求めることができるようになっています。

よって、三角形の集合である「釘ゲージ全体の玉の流れの確率」は、それぞれの「三角形の確率の掛け算と足し算の組み合わせ」で求めることができます。

以上が、玉の流れを確率的に考える際に基本となる考え方。

実際には、パチンコ台盤面のゲージ全体をいくつかのパーツに分けて、この考え方を適用していくことになります。

ワープが付いていないパチンコ機種の「ヘソ入賞確率」

先ずは、簡単のため、ワープが付いていないパチンコ機種を考察してみましょう。

このパチンコ台のゲージを、次の三つのパーツに分けてみます。

• 肩のバラ釘部分
• 寄り部分
• 寄り部分からヘソ

上の三つの部分は、一度、玉が外に逃げると、絶対にヘソ入賞に係らなくなるという非常に重要な振り分けポイント。

この時、このパチンコ台の「ヘソ入賞確率」は以下の式で表されます。

（ヘソ入賞確率） ＝ （肩のバラ釘部分の振り分け率）×（寄り部分の振り分け率）×（寄り部分からヘソへの入賞確率）

ヘソ入賞確率は、三つの部分それぞれの確率の掛け算で求めることができます。

ワープが付いているパチンコ機種の「ヘソ入賞確率」

次に、一般的なワープが付いているパチンコ台について考察してみます。

この場合、ヘソ入賞に係るルートが二つ存在。即ちそれは、ワープ経由のルートと通常経由のルート。

そして、全体の「ヘソ入賞確率」は、これらの足し算になることが分かります。式で表すと、以下のようになります。

（ヘソ入賞確率） ＝ （ワープ通過率）×（ワープからヘソへの入賞確率）＋（ワープ非通過率）×（肩のバラ釘部分の振り分け率）×（寄り部分の振り分け率）×（寄り部分からヘソへの入賞確率）

ヘソ入賞確率を求めるときに重要なこと

「ワープが付いているパチンコ台」のように、ヘソ入賞経路が二つあるパチンコ台の「ヘソ入賞確率」を求める際、確率の足し算を用いました。

実を言うと、これには確率論に於ける『全確率の定理』というものを適用しています。

(参考ページ) 全確率の定理とベイズの定理

つまりパチンコ盤面上の釘配列のゲージに於いて、ヘソ入賞経路が例えいくつあろうとも、この『全確率の定理』によって、それぞれのルートからの入賞率の足し算の総計が、全体のヘソ入賞確率となるのが分かります。

パチンコ台の回転率は、「ヘソ入賞確率」によって決定付けられます。そして、その「ヘソ入賞確率」を求めるのに『玉の流れを確率的に捉える』ことの重要性に触れました。最終的に、確率を求める際には、『全確率の定理』が決定的に重要であることについても書かせて頂きました。

以上のことは、『一般入賞口が完全に潰されている』ことを前提としたお話です。つまり「ヘソ入賞確率」の計算に、一般入賞口からの戻り玉数のことが考慮されていません。理論としては未だ不完全なものであると言えます。

今後のコラムでは、この辺りのことを網羅したお話をして行くつもりでいます。

確率の説明の途中で、若干、抽象的で分かり辛い面もあったかもしれませんが、お付き合い下さりありがとうございました。