【ボーダー理論】パチンコの期待値の求め方を詳しく解説してみる

さて、パチンコの実際の期待値を計算するにあたり、出発点となるのがデジタル1回転あたりの期待値の計算となります。

これは、デジタルを1回転させた時に、一体どのくらいの収益を平均的に得ることが出来るのかということを数値化したものです。（別名、回転単価と呼ばれています）

この計算は、「大当たり1回あたりの平均出玉」、「トータル確率」、「千円あたりのデジタル回転数（回転率）」などを使って、以下のように求めることが出来ます。

（参考）パチンコ用語

まずは、持ち玉で遊技している時のデジタル1回転あたりの期待値の計算式を示してみました。

ここで使われている「トータル確率」というのは、実際には「トータル確率の分母」、つまり「トータル確率の逆数」のことです。（雑誌やサイトに載っているトータル確率というのは実際にはトータル確率の逆数）

さて、次の2つの基本的なことを、まずは確認しておきましょう。

• トータル確率分のデジタルを回した時、大当たり1回あたりの平均出玉を得ることが出来る。
• 千円あたりのデジタル回転数分のデジタルを回した時、250個のパチンコ玉が消費される。

その上で、デジタルを1回転させた時に何が起きるのかを考えてみると、分かり易くなると思います。

つまり、デジタルを1回転させた時の収入としては 式Iの①、支出としては 式Iの②の部分が対応しています。

これらは、パチンコの玉数ベースなので、それぞれ換金率を掛ければ金額ベースに換算できるということになります。

一例を挙げてみましょう。「大当たり1回あたりの平均出玉」が1500個、「トータル確率」が100、「千円あたりのデジタル回転数」が20回転、換金率が3円のパチンコ台の回転単価はいくらになるか？

式Iの①にこれらの数値を代入すると、1500÷100×3－250÷20×3＝7.5となり、この台の持ち玉時の回転単価は7.5円であることが計算できます。

次に、現金投資時のデジタル1回転あたりの期待値を求めてみましょう。

この場合は、式Iの②の部分に掛ける換金率を4円に変えるだけです。

以下に計算式を示しておきます。

基本的な考え方は、式Iと同じ。しかし、②の支出部分のパチンコ玉数に掛ける換金率は、現金投資であることを考慮して、4円にすることが必要になります。

再び先ほどのパチンコ台を例に取って、式Jに数値を代入して計算すると、1500÷100×3－250÷20×4＝－5となり、この台の現金投資時の回転単価は－5円であることが分かります。

実を言うと、もう既に前章で求めた計算式にデジタル回転数を掛けるだけで、その回転数を回した時の期待値は計算できることになっています。

つまり、持ち玉遊技時の時給を求めたいならば、式Iに1時間で回せるデジタル回転数を掛ければ良いし、現金投資時の時給を求める際には式Jで、同様の計算が可能となります。

ところが実際のホール稼働においては、持ち玉遊技と現金投資の状態が混在しているので、これを考慮に入れなければなりません。

それには、持ち玉比率というものが必要になります。持ち玉比率は、デジタル総回転数に対する持ち玉遊技回転数の割合のことです。

それでは、持ち玉比率を考慮した期待値の計算式を以下に示しておきます。

上の式で行っていることは、まずデジタル S 回転の内で、現金投資で回した回転数と持ち玉で回した回転数に分け、それぞれを 式I と 式J に掛けて、足し合わせているだけです。

持ち玉比率は、デジタル回転数によって変化していきます。一般的には、デジタル回転数が大きいと持ち玉比率も大きくなり、デジタル回転数が小さいと持ち玉比率も小さくなります。

アプリやWEBサイト上の期待値計算ツールなどは、上で示した期待値の計算式を元にして作られています。

最後に一つ、パチンコの期待値に関する、少し面白い話題を取り上げてみることにしましょう。

多少技巧的になってしまいますが、前章の 式K を千円あたりのデジタル回転数 R の関数であるとみなして、R で微分してみます。

これは、期待値を「千円あたりのデジタル回転数」の関数とみなした場合の、接線の傾きとなります。

平たく言うと、「千円あたりのデジタル回転数」が1回転変化した時に、期待値がどれだけ増減するのかということです。

さて、具体的に数値を代入してみましょう。等価交換で、千円あたりのデジタル回転数が20回転、デジタル総回転数2000回転のパチンコ台の場合ではどうなるでしょうか？

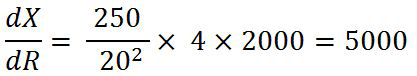
この場合、デジタル回転数が1回転増えると、期待値は5000円程度増加することが分かります。

こうしてみると、期待値の計算式一つ取ってみても、結構色々なことが見えてくるものだと言うことが分かりますね。

ボーダー理論の実践においては、期待値の計算が重要になってきます。

ツールやアプリで計算するのも良いですが、自分で計算したりエクセルなどで管理する場合は、元の期待値の計算式を知っておいた方が役に立つこともあるかと思います。

そんなわけで、今回のコラムは期待値の計算式を詳しく取り上げてみました。